Đường tròn nội tiếp, ngoại tiếp của tam giác là những kiến thức hình học cơ bản được giới thiệu tới các em học sinh trong chương trình Toán lớp 9. Kiến thức trong sách giáo khoa đã tương đối đầy đủ. Trong bài viết này, chúng tôi sẽ tóm tắt và bổ sung thêm các ý chính của phần hình học này và chia sẻ tới các em cách tìm tọa độ tâm đường tròn ngoại tiếp, nội tiếp tam giác. Mời các em học sinh cùng theo dõi để hiểu rõ nội dung phần bài học này nhé.
Định nghĩa đường tròn ngoại tiếp tam giác là gì?
Đường tròn ngoại tiếp tam giác xảy ra khi đường tròn này sẽ đi qua cả 3 đỉnh của một tam giác. Hay có thể gọi theo cách khác là tam giác nội tiếp đường tròn.
Khi đã làm quen với khái niệm đường ngoại tiếp tam giác học sinh sẽ được tìm hiểu thêm về khái niệm đường trung trực. Đường trung trực được định nghĩa như sau:Đường trung trực của đoạn thẳng AB là đường thẳng đi qua trung điểm H của AB đồng thời vuông góc với AB. Khoảng cách từ mọi điểm M nằm trên trung trực đến hai điểm A và B luôn bằng nhau, có nghĩa là MA=MB.
Khái niệm về đường tròn nội tiếp tam giác?
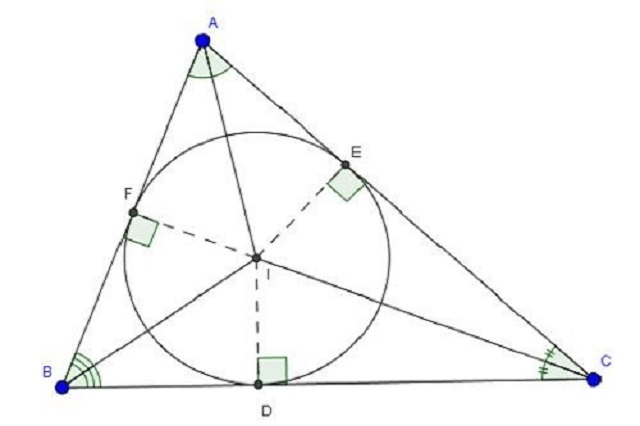
Đường tròn nội tiếp tam giác là khái niệm được nhắc đến trong toán hình học. Đường tròn được xem là nội tiếp tam giác khi đường tròn này nằm trong tam giác và 3 cạnh của tam giác đó là tiếp tuyến của đường tròn.
Cách tìm tọa độ tâm đường tròn nội tiếp, ngoại tiếp tam giác
Muốn tìm tọa độ tâm đường tròn ngoại tiếp tam giác và tâm đường tròn nội tiếp tam giác tiếp các em học sinh cần lưu ý phần đã nêu trong lý thuyết:
- Tâm đường tròn nội tiếp tam giác là điểm mà ba đường phân giác bên trong của tam giác cùng đi qua (cũng có thể là giao điểm 2 đường phân giác)
- Tâm đường tròn ngoại tiếp tam giác là vị trí giao nhau của ba đường trung trực của tam giác đó (cũng có thể là giao điểm 2 đường trung trực).
Một số dạng bài tập về đường tròn ngoại tiếp tam giác
Xác định tọa độ tâm đường tròn ngoại tiếp tam giác trong các trường hợp dưới đây:
Tại mặt phẳng Oxy cho tam giác ABC với A ( 5 ; 7 ) ; B ( 2 ; 9 ) ; C ( – 2 ; – 1 )
Tại mặt phẳng Oxy cho 3 điểm với A ( – 5 ; – 7 ) ; B ( 5 ; – 9 ) ; C ( 2 ; 1 )
Cho đường thẳng (O) đi qua ba điểm A, B và C. Lập phương trình đường thẳng đi qua 3 điểm:
- Bước 1: Gọi phương trình của đường tròn là (C): x2 + y2 – 2ax – 2by + c = 0 (*) (với điều kiện a2 + b2 – c > 0).
- Bước 2: Ta có điểm A; B và C được nằm trên một đường thẳng nên khi thay số liệu của tọa độ các điểm A, B, C vào (*) ta được hệ phương trình ba ẩn a; b; c.
- Bước 3: Giải iải hệ phương trình ba ẩn a; b; c ta được phương trình của đường tròn.
Ví dụ minh họa
Ví dụ 1: Tìm tọa độ tâm đường tròn ngoại tiếp đi qua 3 điểm A (0; 4); B (2; 4) và C (4; 0)
- (0; 0)
- (1; 0)
- (3; 2)
- (1; 1)
Hướng dẫn cách giải
Phương trình đường tròn (C) được viết dưới dạng :
x2 + y2 – 2ax – 2by + c = 0 ( với điều kiện a2 + b2 –c> 0)
Do 3 điểm A; B; C thuộc (C) từ đó viết phương trình đường tròn đi qua 3 điểm (đường tròn ngoại tiếp tam giác)
Suy ra, tâm I (1; 1). Chọn đáp án D
Ví dụ 2: Tâm đường tròn qua ba điểm A (2; 1); B (2; 5) và C (-2; 1) thuộc đường thẳng có phương trình
- A. x – y + 3 = 0.
- B. x + y – 3 = 0
- C. x – y – 3 = 0
- D. x + y + 3 = 0
Hướng dẫn cách giải
Phương trình đường tròn (C) được viết với dạng như sau:
x2 + y2 – 2by + c – 2ax = 0 (a2 + b2 – c> 0)
Viết phương trình đường tròn được đi qua 3 điểm (đường tròn ngoại tiếp tam giác) ⇒ I (0; 3)
Vậy tọa độ tâm của đường tròn là I (0; 3).
Lần lượt thay tọa độ I cho các phương trình có trong đều bài, chỉ có đường thẳng
x – y + 3 = 0 là thỏa mãn .
Vì vậy chọn đáp án A.
Trên đây là khái niệm về đường tròn ngoại tiếp và nội tiếp của tam giác, cách tìm tọa độ tâm đường tròn nội tiếp, ngoại tiếp tam giác. Phương pháp giải một số dạng bài tập về đường tròn ngoại tiếp tam giác mà học sinh lớp 9 cần nhớ. Đây là dạng bài tập quan trọng trong chương trình Toán hình học lớp 9. Nắm vững kiến thức và vận dụng tốt vào các dạng bài tập sẽ giúp các em đạt kết quả cao trong các bài kiểm tra, bài thi cuối kì.
